JavaScriptで二分探索木

December 11, 2021

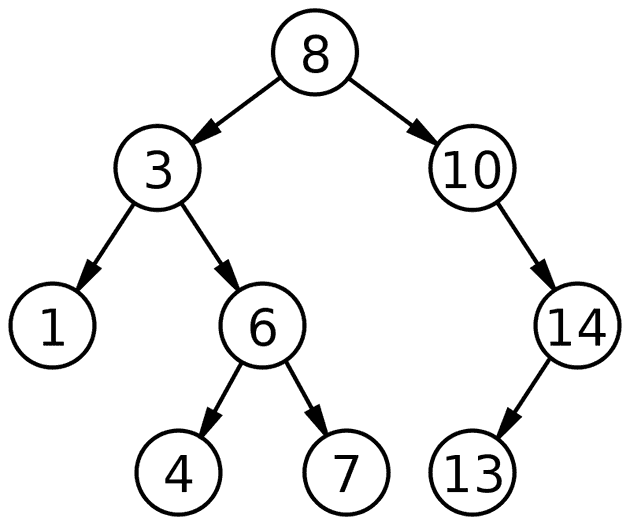
二分探索木とは

wikipediaでは以下のように説明されています。

コンピュータプログラムにおいて、「左の子孫の値 ≤ 親の値 ≤ 右の子孫の値」という制約を持つ二分木である。探索木のうちで最も基本的な木構造である。

単純な直列の配列から目的の値を全件走査で見つけるのは計算量が多い(O(N))ので、二分探索木のように多次元的に管理して効率良く値を見つける(O(logN))というものだそうです。（但し、 O(logN) は二分探索木が理想的な形になっている時であり、保証はされない）

操作

検索

ルートノードから以下の操作を繰り返し、目的のノードを見つける

目的の値が、現在見ているノードの値よりも小さい場合は左のノードを、大きい場合は右のノードを見に行く

挿入

検索操作と似ていますが、ルートノードから以下の操作を繰り返し、ノードを挿入する。

挿入する値が、現在見ているノードの値よりも小さい場合は左のノードを、大きい場合は右のノードを見に行く。次のノードが存在しない場合、そこにノードを挿入

二分探索木にはこれに加え、削除の操作もありますが、検索と挿入に比べ複雑になるので、最後に説明することにする。

二分探索木の実装例

JavaScriptで実装したものが以下

	class Node {
	constructor(value) {
	this.value = value
	this.left = undefined
	this.right = undefined
	}
	}

	Node.prototype.setLeft = function (node) {
	this.left = node
	}

	Node.prototype.setRigth = function (node) {
	this.right = node
	}

	Node.prototype.unsetLeft = function () {
	this.left = undefined
	}

	Node.prototype.unsetRigth = function () {
	this.right = undefined
	}

	Node.prototype.min = function () {
	return this.left ? this.left.min() : this
	}

	Node.prototype.max = function () {
	return this.right ? this.right.max() : this
	}

	Node.prototype.insert = function (node) {
	if (this.value < node.value) {
	this.right ? this.right.insert(node) : this.setRigth(node)
	} else if (this.value > node.value) {
	this.left ? this.left.insert(node) : this.setLeft(node)
	} else {
	console.log(`value:${node.value} is already exists`)
	}
	}

	Node.prototype.find = function (value) {
	if (this.value < value) {
	return this.right && this.right.find(value)
	} else if (this.value > value) {
	return this.left && this.left.find(value)
	} else {
	return this
	}
	}

	Node.prototype.remove = function (value) {
	if (this.left && this.left.value === value) {
	if (this.left.left && this.left.right) {
	const replacement = this.left.left.max()
	this.left.remove(replacement.value)
	this.setLeft(replacement)
	} else if (this.left.left) {
	this.setLeft(this.left.left)
	} else if (this.left.right) {
	this.setLeft(this.left.right)
	} else {
	this.unsetLeft()
	}
	} else if (this.right && this.right.value === value) {
	if (this.right.left && this.right.right) {
	const replacement = this.right.left.max()
	this.right.remove(replacement.value)
	this.setRigth(replacement)
	} else if (this.right.left) {
	this.setRigth(this.right.left)
	} else if (this.right.right) {
	this.setRigth(this.right.right)
	} else {
	this.unsetRigth()
	}
	} else {
	this.left && this.left.remove(value)
	this.right && this.right.remove(value)
	}
	}

view raw BinarySearchTree.js hosted with ❤ by GitHub

上で紹介した insert, find と後で説明する remove 、これらに加えて、二分探索木には、最小値は一番左、最大値は一番右に来るという性質があるので、それを利用して最小値と最大値をそれぞれ返す min, max というメソッドも実装した。

動かしてみる

const root = new Node(8)
const values = [3, 10, 6, 14, 7, 1, 4, 13]
values.forEach(v => root.insert(new Node(v)))

console.log("min", root.min().value) // → 1
console.log("max", root.max().value) // → 14
console.log(root.find(14)) // Node { value: 14, left: Node, right: undefied}
console.log(root.find(2)) // → undefined

削除操作

最後に削除操作について説明していく。

まず、検索操作の要領で削除するノードを見つける。その削除ノードによって操作は以下の3つのケースに分かれる。

削除ノードに子ノードがなかった場合、この時は単純にそのノードを削除する。
削除ノードに子ノードが1つだけあった場合、この時はその子ノードを削除ノードの場所に置き換える
削除ノードに子ノードが2つ合った場合、この時は削除ノードの左のルートの中で最大値を持つノードを見つけ、そのノードを削除ノードの場所に置き換える。

この削除操作を実装したものが以下。

Node.prototype.remove = function (value) {
  if (this.left && this.left.value === value) {
    if (this.left.left && this.left.right) {
      const replacement = this.left.left.max()
      this.left.remove(replacement.value)
      this.setLeft(replacement)
    } else if (this.left.left) {
      this.setLeft(this.left.left)
    } else if (this.left.right) {
      this.setLeft(this.left.right)
    } else {
      this.unsetLeft()
    }
  } else if (this.right && this.right.value === value) {
    if (this.right.left && this.right.right) {
      const replacement = this.right.left.max()
      this.right.remove(replacement.value)
      this.setRigth(replacement)
    } else if (this.right.left) {
      this.setRigth(this.right.left)
    } else if (this.right.right) {
      this.setRigth(this.right.right)
    } else {
      this.unsetRigth()
    }
  } else {
    this.left && this.left.remove(value)
    this.right && this.right.remove(value)
  }
}

以上、二分探索木の実装でした。